区块链中的密码学系列之数字证书体系(十四)

2019-04-07 | 阅读：次

1. 前言
2. 密钥分配与密钥管理
3. PKI 体系
3. 基于身份的密码体制

1. 前言

数字证书用来证明某个公钥是谁的，并且内容是正确的。

对于非对称加密算法和数字签名来说，很重要的一点就是公钥的分发。一旦公钥被人替换（典型的如中间人攻击），则整个安全体系将被破坏掉。

解决公钥分发的问题。

怎么确保一个公钥确实是某个人的原始公钥？这就需要数字证书机制。

顾名思义，数字证书就是像一个证书一样，证明信息的合法性。由证书认证机构（ Certification Authority，CA）来签发，权威的 CA 包括 verisign 等。

数字证书内容可能包括版本、序列号、签名算法类型、签发者信息、有效期、被签发人、签发的公开密钥、CA 数字签名、其它信息等等，一般使用最广泛的标准为 ITU 和 ISO 联合制定的 X.509 规范。

文档

版本号Version Number
序列号（Serial Number）:CA维护给每个证书分配的唯一序列号，用于追踪和撤销证书。签发者信息+序列号确定一个证书。
签名算法(Signature Algorithm)
颁发者(Issuer)：颁发证书的单位
- C=CN，国家
- ST=Beijing，省份
- L=Beijing,城市
- O=org.example.cm，网站域名
- CN=ca.org.example.cm，网站域名
证书有效期
- 此日期前无效
- 此日期后无效
主体：证书拥有者信息
主体公钥信息
- 公钥算法
- 主题公钥
颁发者唯一身份信息（可选项）
主体唯一身份信息（可选项）
扩展信息（可选项）

证书的颁发者会使用自己的私钥对证书进行签名，防止别人篡改。

x.509使用pem(Privacy Enhance Mail)格式来存储。证书请求文件的后缀名是csr，私钥文件是key，证书的文件名后缀为crt，cer。

此外，还有der(Distinguished Encoding Rules)格式，可以与pem格式进行转换。

我们来实际的看一个：

然后用openssl来查看内容：

openssl x509 -in example.com-cert.pem -noout -text

其中，最重要的包括签发的公开密钥，CA 数字签名（证书颁发者使用自己的私钥签名）两个信息。因此，只要使用CA颁发者的公钥对这个证书验证，就能证明某个公钥是合法的，因为带有 CA 的数字签名。

更进一步地，怎么证明 CA 的签名合法不合法呢？

类似的，CA 的数字签名合法不合法也是通过 CA 的证书来证明的。主流操作系统和浏览器里面会提前预置一些 CA 的证书（承认这些是合法的证书），然后所有基于他们认证的签名都会自然被认为合法。主要是证书信任链。

2. 密钥分配与密钥管理

2.1 密钥管理概述

密码系统的两个基本要素是加密算法和密钥管理。加密算法是一些公式和变换，它规定了明文和密文之间的变换方法。由于密码系统的反复使用，密钥是控制加密算法和解密算法的关键信息，用户必须建立双方的共享密钥来支持他们的安全通信。

密钥管理是指对密钥生命周期的全过程(产生、存储、分配、归档、使用、废除、销毁)实施的安全保密管理，满足保密系统的安全使用。

2.2. 单钥加密体制的密钥分配

2.2.1 密钥分配的基本方法

通过物理手段，通过安全信道进行传输，通过密钥协商算法共享密钥。

2.2.2 密钥的分层控制

KDC：密钥分发中心。

网络中如果用户数目非常多或分布地域非常广，一个KDC无法承担为用户分配密钥的重任，可采用多个KDC的分层结构来解决该问题。

分层结构可减少主密钥的分布，分层结构还可将虚假KDC的危害限制到一个局部区域。

2.2.3 密钥的控制使用

密钥按其用途分为密钥加密密钥(包括主密钥)和会话密钥。

Δ 会话密钥是用来直接对数据加密的密钥，是最底层的密钥，又称数据加密密钥或工作密钥;

Δ 密钥加密密钥对密钥进行加密，是最底层以上的所有密钥，用来保护其它密钥。

Δ 主密钥:最顶层的密钥，是密钥系统的核心。

密钥标签:用于DES的密钥控制，将DES的64比特密钥中的8个校验位作为控制使用这一密钥的标签。

一个bit:会话密钥还是主密钥
一个bit:能否用于加密
一个bit:能否用于解密
其他bit:无特定含义，留待以后使用
备注:标签在密钥中，与密钥一起被加密，可保护标签。缺点:有长度限制，降低了灵活性和功能;标签解密后才能使用，限制了对密钥使用的控制方式

控制矢量(比标签灵活)

对每一会话密钥指定一个相应的控制矢量
分为若干字段，分别用于说明在不同情况下密钥是否被允许使用
长度可变
控制矢量实在KDC产生密钥时加在密钥中
H=h(CV)
Kin=Km⊕H
Kout=EKm ⊕ H[Ks]
Ks=DKm⊕ H[EKm⊕ H[Ks]]
KDC在向用户发送会话密钥时，同时以明文形式发送控制矢量IV。用户只有使用与KDC共享的主密钥及IV才能恢复会话密钥KS，所以需要保留KS和它的IV之间的对应关系。

2.3 基于公钥加密体制的密钥建立

2.3.1 公钥的分配

由于公钥密码体制加密速度慢，在保密通信中不直接用于大数据的加密，主要用于密钥管理和认证。

公开发布：用户将自己公钥发给其他用户，或向某一团体广播。如:PGP中(RSA算法)，用户将公钥附加到消息上，然后公开到公共区域，如因特网邮件列表中。
公用目录表：管理员建立一个公用的公钥动态目录表(建立、维护、更新目录)(缺点:管理员易受攻击，密钥泄露)
公钥管理机构：用户向该机构请求其他用户公钥。
公钥证书：用户之间互相交换证书来获得公钥。

2.3.2 用公钥加密分配单钥密码体制的的密钥

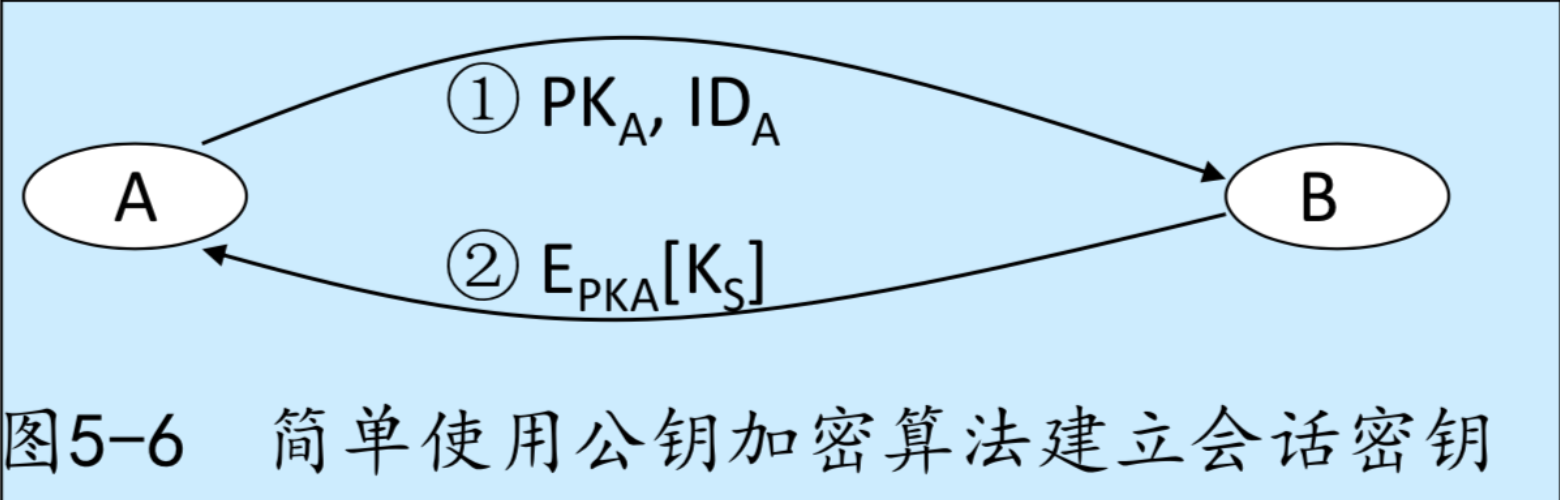
图5-6的协议可以用文字描述如下: 协议5-6 简单使用公钥加密算法传输会话密钥

A→B: PKA, IDA
B→A: EPKA[KS]

分析:由于图5-6中的协议5-6在B返回的消息中使用的加密机制，被动攻击者通过搭线窃听无法获得会话密钥KS。

但是该协议不能抵抗主动攻击者，见攻击5-6 ́。

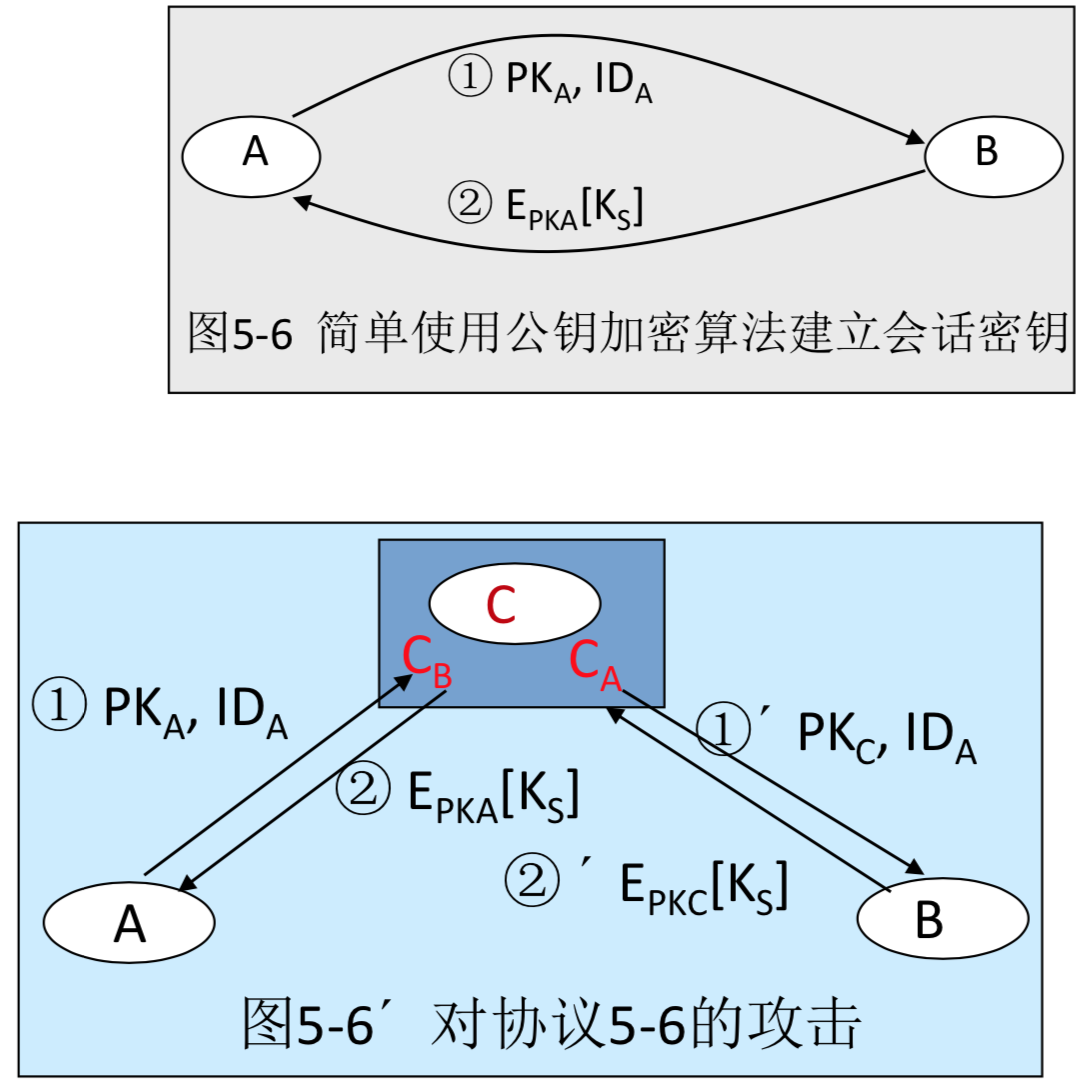
在攻击5-6 ́完成后，A与B建立了共享会话密钥KS，但C也知道KS。

这是公钥和身份没有绑定的缺陷。

2.3.3 Diffie-Hellman密钥交换协议

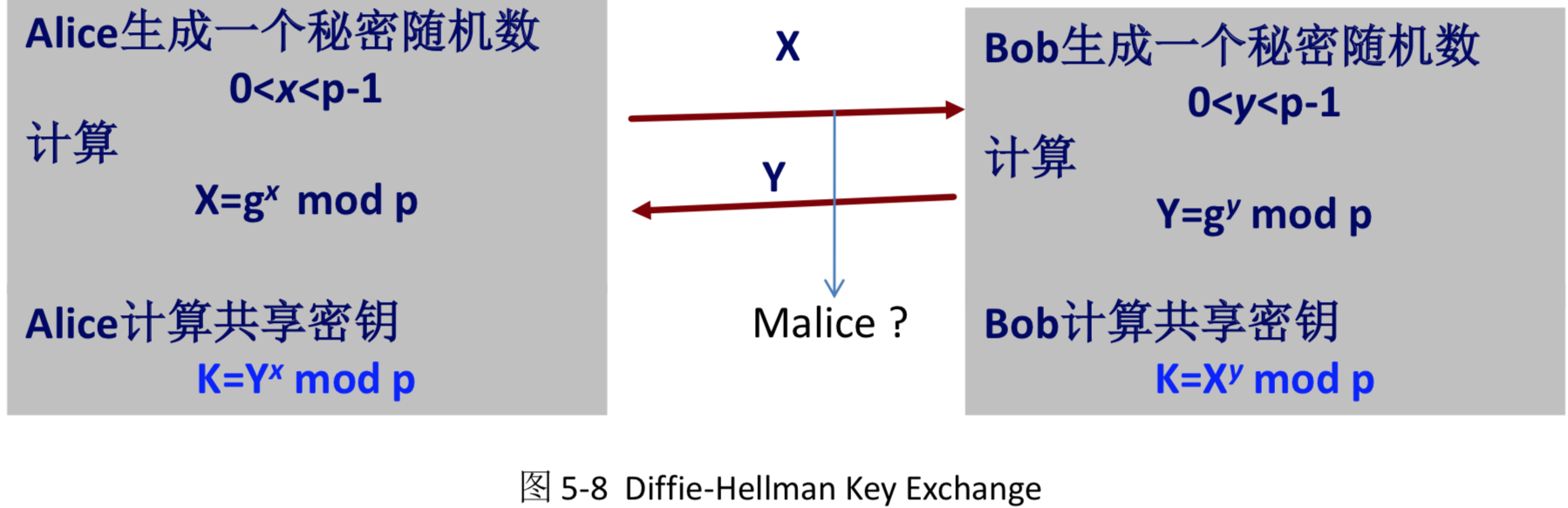
事先Alice与Bob(或多主体)约定一个公开的大素数p和一个大整数g，满足1<g<p(这里p,g公开且所有用户可共同使用)。

2.4 密钥托管

提出托管加密标准EES。

2.5 随机数的产生

2.5.1 随机数的使用

随机数在密码学中占有重要地位，可作为加密系统中的密钥(会话密钥、公钥算法中的私钥)、安全协议中的一次性随机数、身份认证等。

2.5.2 伪随机数产生器

最为广泛使用的伪随机数产生器是线性同余算法

Xn+1=(aXn+c)mod m
- 迭代算法，a、c、m的取值是产生高质量随机数的关键
- 为使随机数数列的周期尽可能大，m应尽可能大，可选计算机能表示的最大整数，如接近或等于2^31
线性同余算法的评价标准
- 迭代函数是整周期的
- 产生的数列看上去应是随机的
- 迭代函数能有效地利用32位运算实现

2.5.3 基于密码算法的随机数产生器

通常分组密码或流密码具有良好统计和抗分析特性，很多随机数生成器使用这些密码算法来生成实际可用的随机数。

通过循环加密或者分组密码DES的输出反馈模式(OFB)。

2.5.4 随机比特产生器

BBS(Blum-Blum-Shub)随机数产生器，已经过证明的密码强度最强的伪随机数产生器。

首先，选择两个大素数p,q,满足p≡q≡3(mod 4)，令n=pq。再选一随机数s，使得s与n互素。然后按以下算法产生比特序列{Bi}:

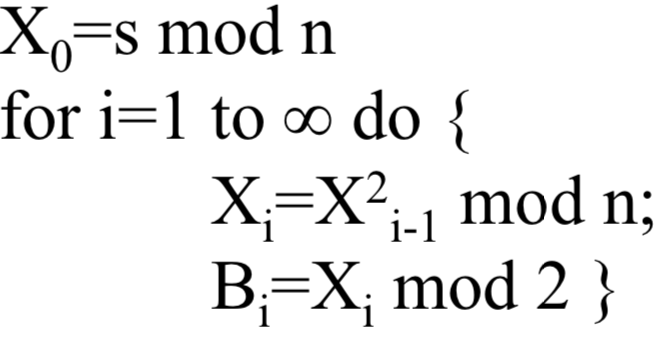
即在每次循环中取Xi(i=1,2,…)的最低位。

已知一个序列的前k个比特，不存在实际可行的算法能以大于1/2的概率预测下一比特是0还是1。

2.6 秘密分享

秘密分享(Secret sharing)是指多个参与者共同分享一个秘密，每个参与者拥有该秘密的一个份额，只有足够数量的份额联合才能回复该秘密，任何单个或部分份额无法恢复秘密。

A. Shamir和G. Blakley提出了秘密共享概念，并给出(t, n)门限秘密共享体制。

2.6.1 门限方案的一般概念

设秘密s被分成n个信息份额，每一部分信息称为一个子秘密或影子(shadow)，由一个参与者持有，使得:

由k个或多于k个参与者所持有的子秘密可重构s。
由少于k个参与者所持有的部分信息则无法重构s。

则称这种方案为(k,n)秘密分享门限方案，k称为方案的门限值。如果3 由少于k个参与者所持有的子秘密得不到秘密s的任何信息。则称这个方案是完善的，即(k,n)-秘密分享门限方案是完善的。

2.6.2 Shamir门限方案

Shamir门限方案基于多项式的Lagrange插值公式。

设{(x1,y1),…,(xk,yk)}是平面上k个点构成的点集，其中 xi(i=1,…,k)均不相同，那么在平面上存在一个惟一的k- 1次多项式f(x)通过这k个点。若把密钥s取作f(0)，n个子密钥取作f(xi)(i=1,2,…,n)，那么利用其中的任意k个子密钥可重构f(x)，从而可得密钥s。

插值多项式

定理(唯一性) :满足f(xi)=yi, xi≠xj (i≠j), i, j=1, …, k的(k-1)次多项式是唯一存在的。

事实上，设f(x)的表达式为f(x)=a0+a1x+…+a(k-1)x^(k-1)。

由已知条件， f(xi)=yi, xi≠xj(i≠j),i=1,…,k 得到如下线性代数方程组:

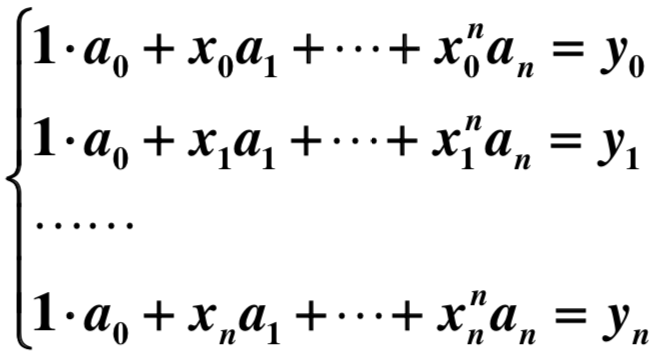
(k,n)秘密分享门限方案

(1) 选择k-1次多项式

设GF(q)是一有限域，满足q≥n+1，秘密s∈RGF(q) {0}。 k-1个系数a1,a2,…,ak-1的选取也满足ai∈RGF(q) {0}(i=1,2,…,k-1)。在GF(q)上构造一个k-1次多项式

f(x)=a0+a1x+…+a(k-1)x^(k-1)

(2) 秘密份额分发

n个参与者记为P1,P2,…,Pn， Pi分配到的秘密份额为f(i),i=1,…,n。

(3) 秘密重构如果k个参与者希望获得秘密s,可使用{ij,, f(ij)|j=1,2,…,k}执行以下运算:

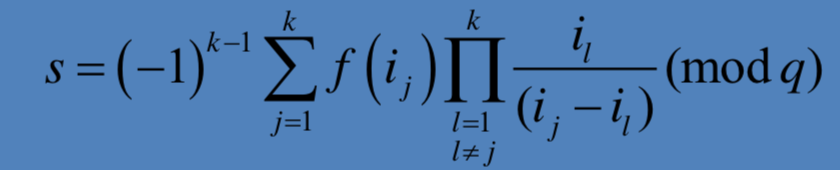
可行性分析:

因为ij (j=1,…,n)各不相同，所以f(x)可以由Lagrange公式重构:

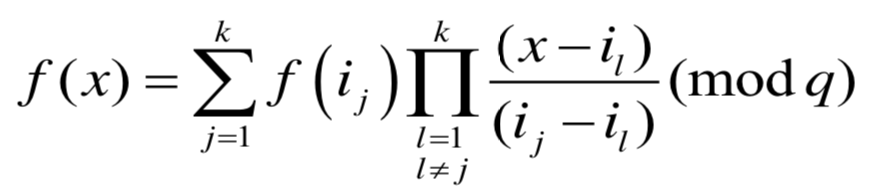
如果少于k，如k-1个成员试图获得秘密s，他们只能构造由k-1个方程组成的线性方程组:

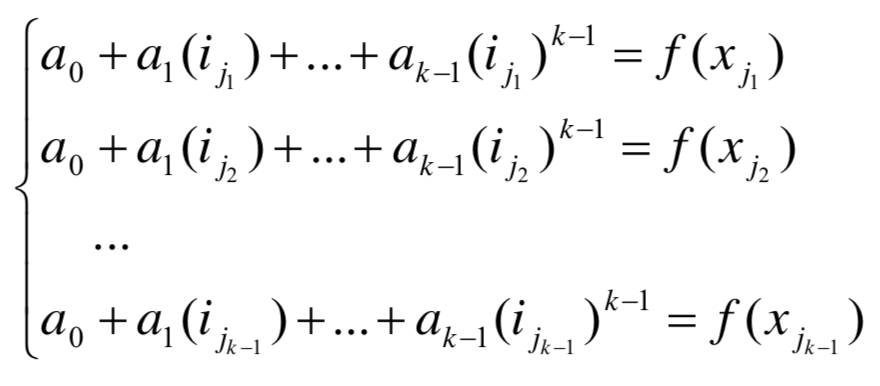
上述方程线性组中有k个未知量，无法获得关于多项式系数和常数项s=f(0)的任何信息。

例子：

设k=3,n=5,q=9,s=11，随机选取a1=2,a2=7，的多项式为 f(x)=(7x^2+2x+11) mod 19

分别计算

f(1)=(7+2+11) mod 19=20 mod 19=1；

f(2)=(28+4+11) mod 19=43 mod 19=5;

f(3)=(63+6+11) mod 19=80 mod 19=4;

f(4)=(112+8+11) mod 19=131 mod 19=17;

f(5)=(175+10+11) mod 19=196 mod 19=6

得5秘密份额1,5,4,17,6，分别秘密分发给五个参与者。

根据Lgrange插值公式，五个参与者中的任何3个成员使用分发的秘密份额可以重构秘密份额。

例如P1,P2,P3将k=3,f(1)=1,f(2)=5,f(3)=4代入Lagrange插值公式。

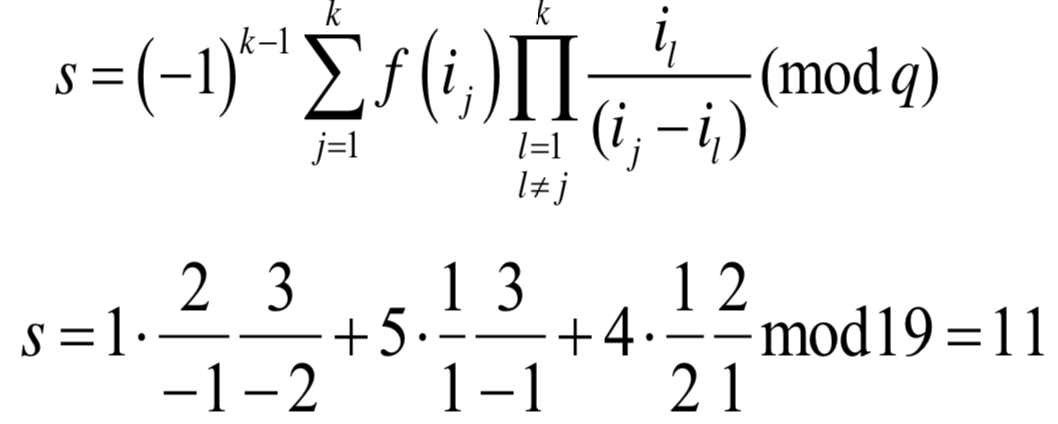
3. PKI 体系

在非对称加密中，公钥则可以通过证书机制来进行保护，如何管理和分发证书则可以通过PKI（ Public Key Infrastructure）来保障。

顾名思义，PKI 体系在现代密码学应用领域处于十分基础的地位，解决了十分核心的证书管理问题。

PKI 并不代表某个特定的密码学技术和流程，PKI 是建立在公私钥基础上实现安全可靠传递消息和身份确认的一个通用框架。实现了 PKI 的平台可以安全可靠地管理网络中用户的密钥和证书，包括多个实现和变种，知名的有 RSA 公司的 PKCS（ Public Key Cryptography Standards）标准和 X.509 规范等。

一般情况下，PKI 至少包括如下组件：

CA（ Certification Authority）：负责证书的颁发和吊销，接收来自 RA 的请求，是最核心的部分；
RA（ Registration Authority）：对用户身份进行验证，校验数据合法性，负责登记，审核过了就发给 CA；
证书数据库：存放证书，一般采用 LDAP 目录服务，标准格式采用 X.500 系列。

CA 是最核心的组件，主要完成对证书的管理。常见的流程为，用户通过 RA 登记申请证书，CA 完成证书的制造，颁发给用户。用户需要撤销证书则向 CA 发出申请。

之前章节内容介绍过，密钥有两种类型：用于签名和用于加解密，对应称为签名密钥对和加密密钥对。

用户证书可以有两种方式。一般可以由 CA 来生成证书和私钥；也可以自己生成公钥和私钥，然后由 CA 来对公钥进行签发。后者情况下，当用户私钥丢失后，CA 无法完成恢复。

3. 基于身份的密码体制

基于身份的加密(IBE , Identity-based Encryption)是不同于传统的PKI(公开密钥基础设施)而发展来的公钥加密机制，主要简化在具体安全应用中大量数字证书的交换和维护等问题。IBE中任意的数据串均可作为公钥，这个公钥就是他的身份标识，如E-Mail地址，电话号码等。

这张图的意思是PKG首先生成主公钥和私钥，然后Alice获取主公钥，结合自己的名字生成自己的公钥，，然后PKG根据Alice的公钥生成Alice的私钥。

但是上面的只是一种思想，没有找到合适的工作机制，直到提出基于双线性对（Bilinear Map）的身份密码体制。使用超奇异椭圆曲线(Supersingular Elliptic Curve)上的双线性对(Weil Pairing或Tate Pairing)，有效地实现了基于身份的公钥加密方案。

双线性对是满足e(aX, bY)=e(bX, aY)=e(X,Y)^ab的函数映射。

双线性映射

设q是一个大素数，G1,G2是两个q阶群(通常G1,G2分别为椭圆曲线群和有限域上乘法群)，其上的运算分别为加法和乘法。G1到G2的双线性映射e: G1×G1→G2，满足以下性质:

双线性:对任意P,Q,R∈G1和a,b∈Z，有e(aP, bQ)=e(P, Q)ab，或写成e(P+Q, R)=e(P, R)·e(Q, R)和e(P, Q+R)=e(P, Q)·e(P, R)。
非退化:映射不把G1×G1所有元素映射为单位元。 3 可计算:对任意的P,Q∈G1，e(P, Q)可以有效计算。

其中a,b是整数，P,Q是椭圆曲线上的点，e(P,Q)是普通有限域中元素。

双线性DH问题

定义:双线性DH问题简称为BDH(Bilinear Diffie-Hellman)问题，是指给定(P, aP, bP, cP)(a,b,c∈Zq*)，计算w=e(P,P)^abc∈G2，其中e是一个双线性映射，其中P是G1的生成元，G1,G2是阶为素数q的群。

IBE方案：

令k是安全参数，g是BDH参数生成算法，输出包括素数q(k比特)，两个阶为q的群G1,G2，一个双线性映射e: G1×G1→G2。消息空间为M={0,1}^n，密文空间为C= G1×{0,1}^n 。

An identity-based encryption scheme is specified by four randomized algorithms: Setup, Extract, Encrypt, Decrypt: $\textbf{Setup}$ : takes a security parameter $k$ and returns $params$ (system parameters) and $master\text{-}key$ . The system parameters include a description of a nite message space $\mathcal{M}$ , and a description of a finite ciphertext space $\mathcal{C}$ . Intuitively, the system parameters will be publicly known, while the $master\text{-}key$ will be known only to the “Private Key Generator” (PKG). $\textbf{Extract}$ : Extract: takes as input params, master-key, and an arbitrary $ID\in{0,1}^*$ , and returns a private key $d$ . Here $ID$ is an arbitrary string that will be used as a public key, and $d$ is the corresponding private decryption key. The $\textbf{Extract}$ algorithm extracts a private key from the given public key. $\textbf{Encrypt}$ : takes as input $params$ , $ID$ , and $M\in\mathcal{M}$ , It returns a ciphertext $C \in \mathcal{C}$ . $\textbf{Decrypt}$ : takes as input $params$ , $ID$ , $C \in \mathcal{C}$ , and a private key $d$ , It returns $M \in \mathcal{M}$ .